简介

本文发表于 CVPR 2021，代码见此。

本文从信息论的角度分析了增量学习过程，提出增量学习过程中，模型经验随着模型所看到的数据积累而积累，每个模型的参数推断也应该逐渐趋于确定（数据量的增加使得参数空间逐渐减小，确定性增加，熵减少）。这样，增量学习实际是由顺序传入的任务所驱动的一个递归的学习模型参数信息的过程。从这个观点来看，遗忘可以被理解为先前任务数据提供的关于模型参数信息的丢失。

为了更加直观的研究信息增益（IG, Information Gain），本文对模型参数进行了量化（例如20位字节）让参数以字节的形式展现。对于一个参数而言，在之前的训练中已经确定的位如果在之后的训练中发生了翻转，就意味着舍弃了之前所学习到的信息，从而发生了遗忘。

就本质而言，本文的思想和EWC等正则化方法一致，都是认为确定性高的参数在增量过程中发生改变意味着舍弃过去知识。不过本文通过将参数表示为字节形式，降低了颗粒度，并基于字节形式利用香农熵的变化从数学的角度推断出需要被冻结的bit。这使得本文在思路上和方法上都给人一种耳目一新的感觉。

据此，本文提出了一种新的位级信息保存（BLIP, Bit-level Information Preserving）方法，该方法通过位冻结对模型参数进行量化，并直接保留先前学习任务带来的模型参数信息增益。

bit-level 指的是将权重转换为字节的形式，以高位到地位的顺序逐渐固定字节。相较于freeze parameter，freeze bit 拥有更细的颗粒度，

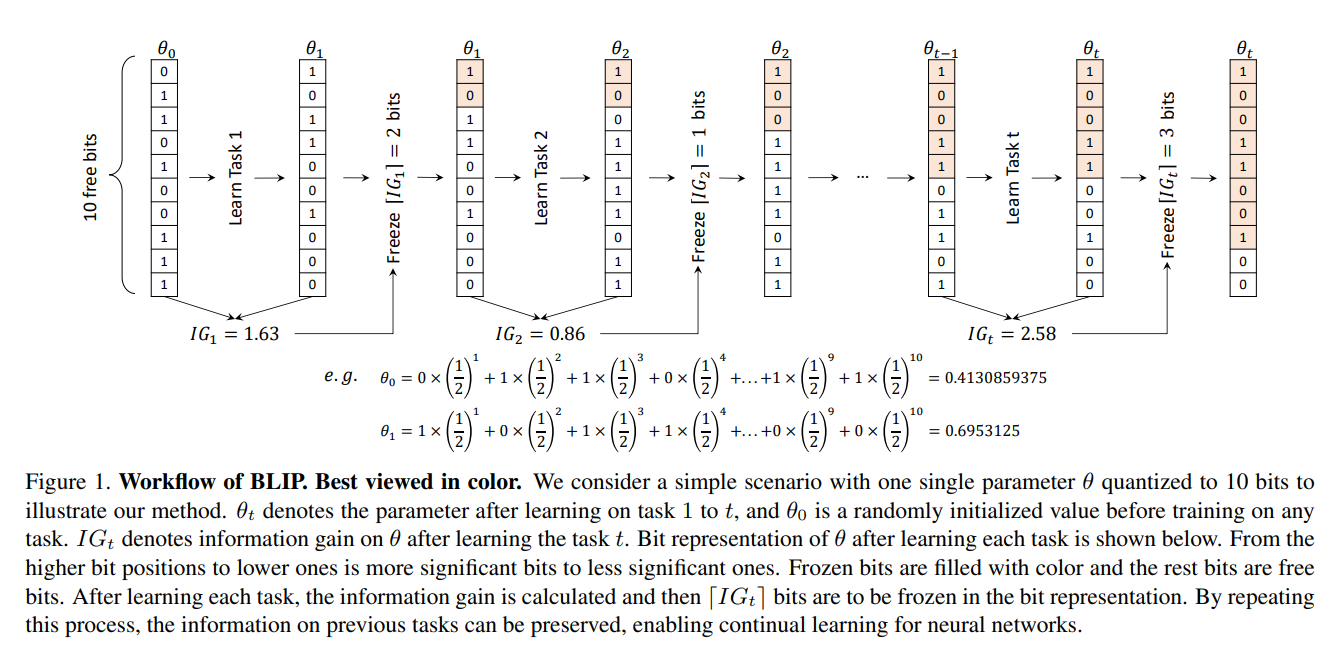
Bit-level Information Preserving

Algorithm 1 给出了完整算法

所以应该怎样 freeze bit 呢？

论文的 section 4.4 给出了在 Information Gain 指导下的 Bit Freezing。信息增益，即学习任务$D_t$后香农熵的减少，因此可以近似的等于过程中$Q(\theta,N)$里有多少更多的bit被确定。这些特定位继续翻转（flip）意味着丢弃已有的信息增益，故需将其冻结。其公式如下：

$$n_t=\lceil IG(Q(\theta,N),D_t)\rceil$$

此外，由于 $\theta$ 上的后验是高斯分布，并且只会在局部变得峰值和集中，因此 $Q(θ, N)$ 中的位从较高的有效位到较低的有效位开始变得确定。

相关的公式如下：

$$IG(Q(\theta,N),D_t)=H(Q(\theta_{0:t-1},N))-H(Q(\theta_{0:t},N))$$

$$H(Q(\theta,N))=-\sum_{i=1}^{2^N}P(Q(\theta,N)=q_i)log_{2}P(Q(\theta,N)=q_i)$$

$$Q(\theta,N)=\frac{\lfloor(2^Nmin(max(\theta,-1+\frac{1}{2^N+1}),1-\frac{1}{2^N+1}))\rceil}{2^N},其中\lfloor~·\rceil将数字舍入到最接近的整数$$

其中$q_i$代表$Q(\theta,N)$在$i$-$th$可能的取值，$N$是位数。为了顺利求导，本文使用了直通估计器（ Straight Through Estimator, STE）[1]，将$Q$的梯度近似为$\frac{\partial Q(\theta,N)}{\theta}=1$。

实验结果

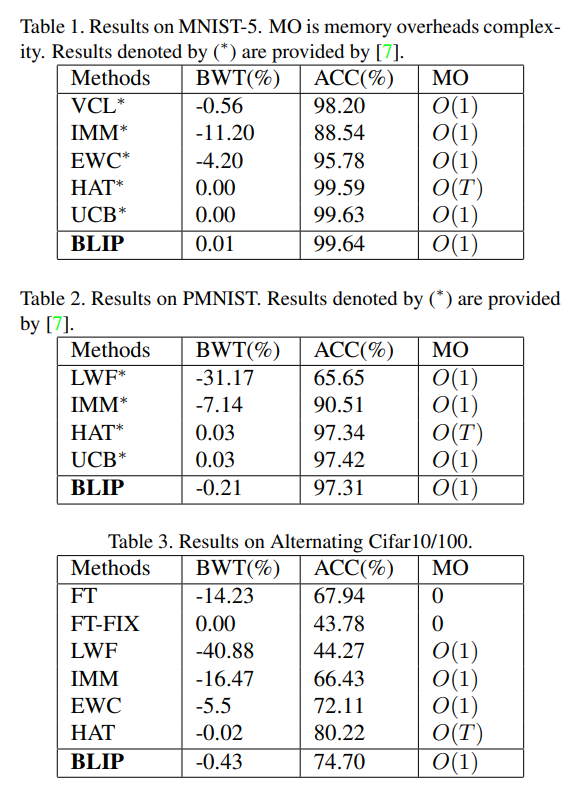
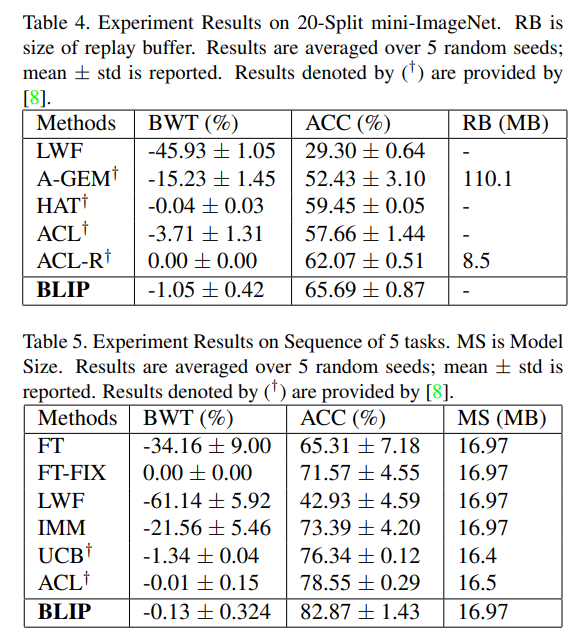
实验结果显示准确率非常高，对于一个没使用 rehearsal 的方法而言这简直是质的飞跃。不过，当看到 Benchmarks and Models 中的"task identity is given during both training and evaluation"，我意识到实际的测试可能要依据task-id。仔细阅读代码后发现本文采用了 multi-head classifier，所以这个准确率比较正常。本文最有趣的地方还是提出的视角颇为新颖。