论文笔记——Efficient Feature Transformations for Discriminative and Generative Continual Learning
简介
本文基于 architectural strategy,聚焦于提高效率(Efficient),即压缩网络模型,降低模型参数。文章照例分析了现有的三种主流策略:rehearsal,regularization和archetectural。指出rehearsal受制于memory buffer,模型新旧任务间的bias严重;regularization则会限制模型的scalability且regularization通常猜想参数的重要性是独立的,而忽略了参数间的相关性(从底层角度,这是因为神经网络的黑盒特性)。而architectral可以从设计(design)上缓解灾难性遗忘,且根据新任务扩充网络可以保证模型的scalability(维护模型结构同时可能避免性能的unintentional degradation,因为许多模型诸如超参数设置等都是在工程上精心设计过的)。而architetural的的一个主要的缺陷是参数量大、性能消耗大,所以本文提出了一种新的特征变换方法,为其命名为 EFT (Efficient Feature Transformation)。
方法
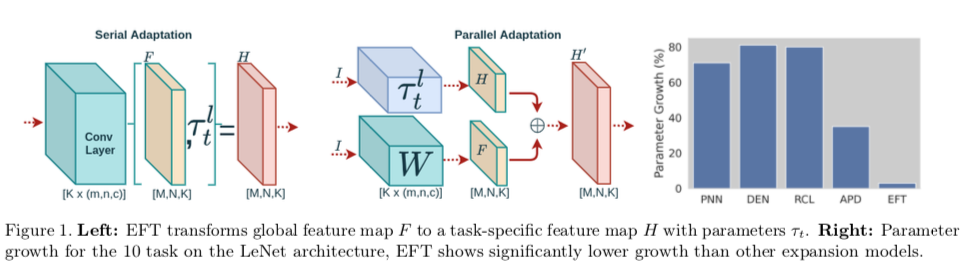
本文将参数分成了glbal parameter $\theta$和task-specific local parameter $\tau_t$,在训练任务t时,$\theta$和$\tau_{1:t-1}$保持不变,只有$\tau_t$被训练。Fig 1 center 是另一种参数化方法,它并行计算这些特征校准,使变换增加而不是合成。公式如下:
$$H^{'}=(WI)\bigoplus(\tau^l_tI)$$
其中$\bigoplus$是增加(addition),$\tau^l_t$是$l-layer$的 task-specific parameter。
2D Convolution Layer
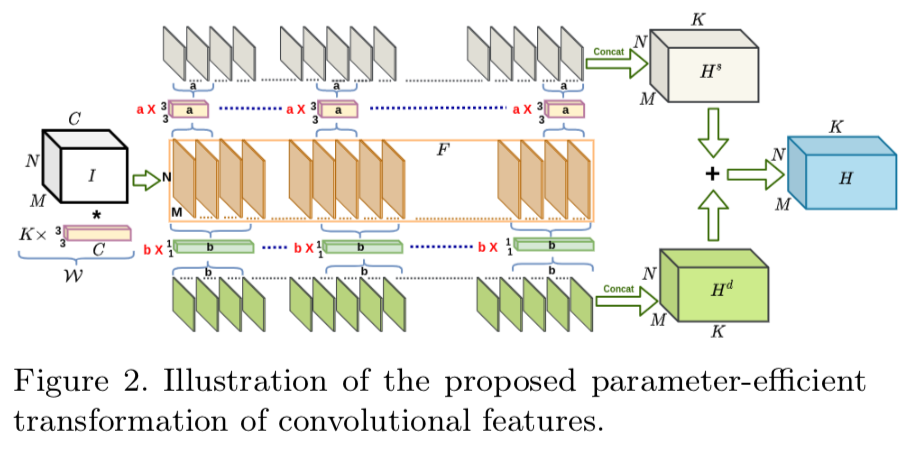
简而言之,EFT设计了两类卷积核 $w^s \in 33a$和$w^d\in11b$分别用于计算特征的空间信息和深度信息。对于一个特征$F$,EFT将其分成了 $K/a$和$K/b$个group,每个group都有对应的$w^s$和$w^d$,将这些分割的特征通过concatenat,并将利用公式$H=H^s+\gamma H^d$就能空间信息和深度信息合成一个完整的feature map $H$了,它的结构与正常卷积的结构一致。公式中$\gamma \in {0,1}$用以指示是否使用 $w^d$。
Fully Connected Layer
和卷积层一样,EFT也设计task-speicfic fully conneted layer,即通过另一个全连接层(由$E$参数化)将输出向量$F$转换为特定于任务的特征向量H。公式为$h=Ef$,为了节省计算开销,其中的$E$为对角矩阵,这让该公式实现了一个Hadamard product。
Task Prediction
对于CIL这种情况,本文采用了通过分类时的最大置信度预测(maximum confidence prediction)的来选择$\tau_t$。然而,由于典型的交叉熵训练目标倾向于在确定性神经网络中产生高置信度(即使对于分布外(OoD, out-of-distribution)样本),故softmax预测熵的简单直接测量通常表现不佳[1]。为了解决这个问题,本文提出了一种简单的正则化方式来最大化特征距离,以提高任务预测能力:
$$L_M=\sum_{i=1}^{t-1}max(\Delta-KL(P_t||Q_i),0)$$
其中 $P_t = N(μ_t,Σ_t) $和 $Q_i = N(μ_i,Σ_i)$ 是当前任务$t$ 和较早任务 $i < t$ 的分布。 该正则化项帮助模型学习 $τ_t$ 的表示,使得当前任务数据 ($D_t$) 在特征空间中与由先前任务的参数 $τ<t$ 编码的特征至少具有$∆$可分离性。
所以,最终的损失函数为:$L_{EFT} =L(yˆ,y)+λL_M$
实验
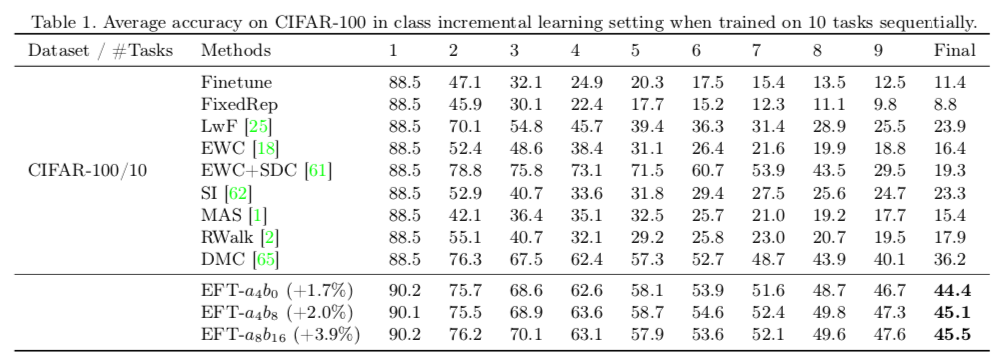
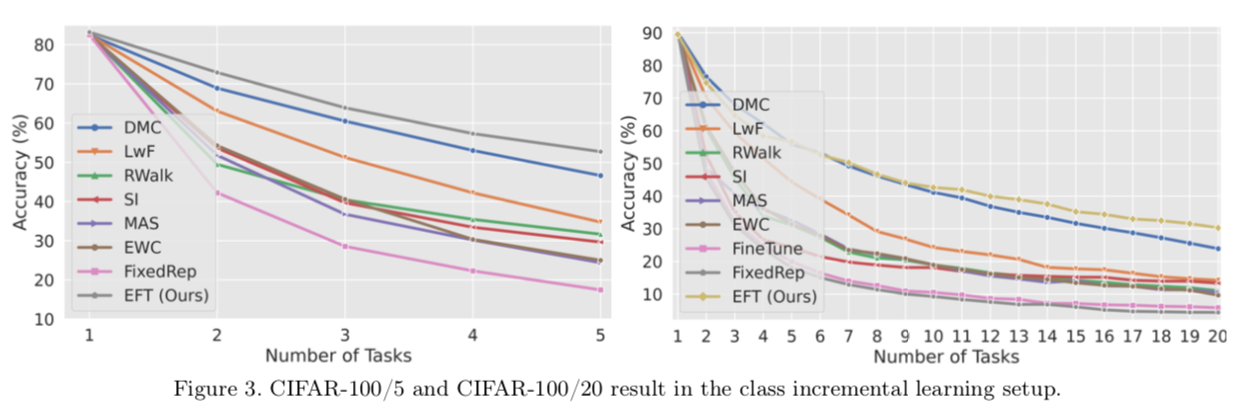
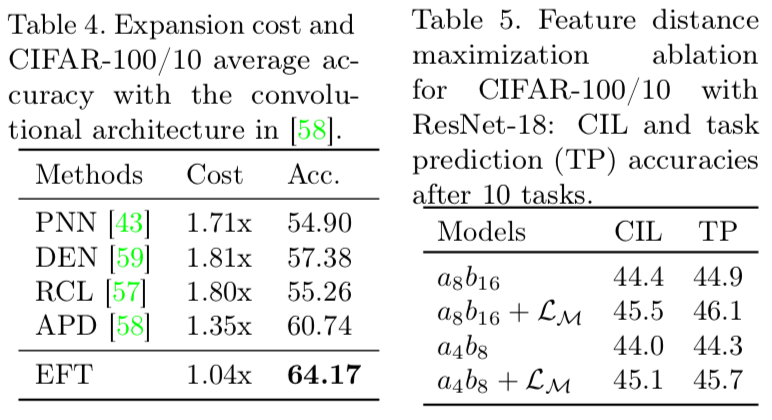
整体而言,本文在想法上基本遵循了之前的思想,并无太大创新,其内核和建筑化策略一致。但本文聚焦于计算效率问题,很大幅度的降低了参数增长,这是本文工作中最杰出的部分。至于建筑化的一些关键缺陷,比如推断时如何找到对应网络,本文依旧没有提出有效的解决方法。(Table 5 说明了$L_m$有作用,但效果很不明显。显然,基于置信度筛选还是非常容易翻车的)