论文笔记——Mnemonics Training: Multi-Class Incremental Learning without Forgetting
简介
本文基于 Rehearsal strategy,从改进样例集的角度出发提出了 Mnemonics Training。他们把旧样例集(exemplars)进行了参数化,在训练过程中从两个层面进行优化:模型层面,数据层面。即不仅模型的参数是可学习的,留存的数据也是可学习的。
训练的思想就是同时优化模型参数和留存数据(交替优化),让模型在数据集上的loss尽可能小。
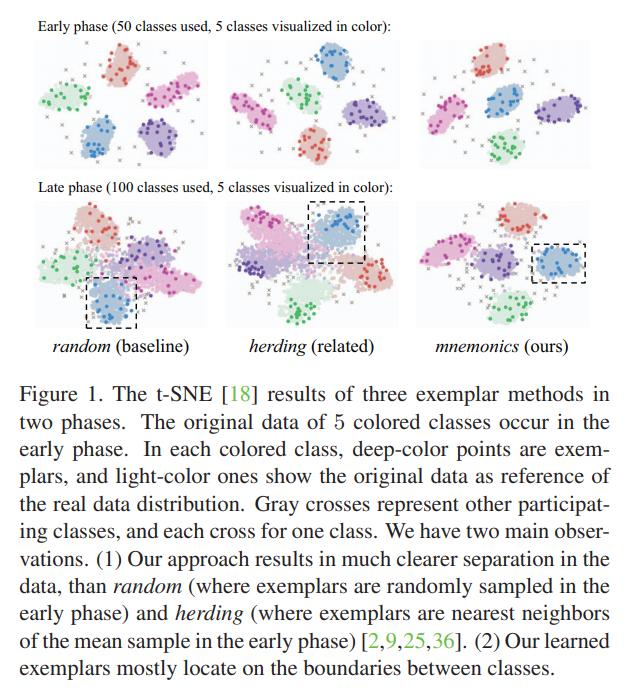
提出 Mnemonics 的背景是其他数据筛选方式(herding, random)的性能并不算好,作者利用TSNE可视化(见fig.1)指出 Mnemonics 相较而言能更好地保存数据的边界信息。(其实这个说法有些奇怪,毕竟对于 herding 而言,其留存的数据集靠近中心是正常现象,因为它就是基于均值进行采样的。不过本文最后的实验结果确实较好,这佐证了作者的论证)
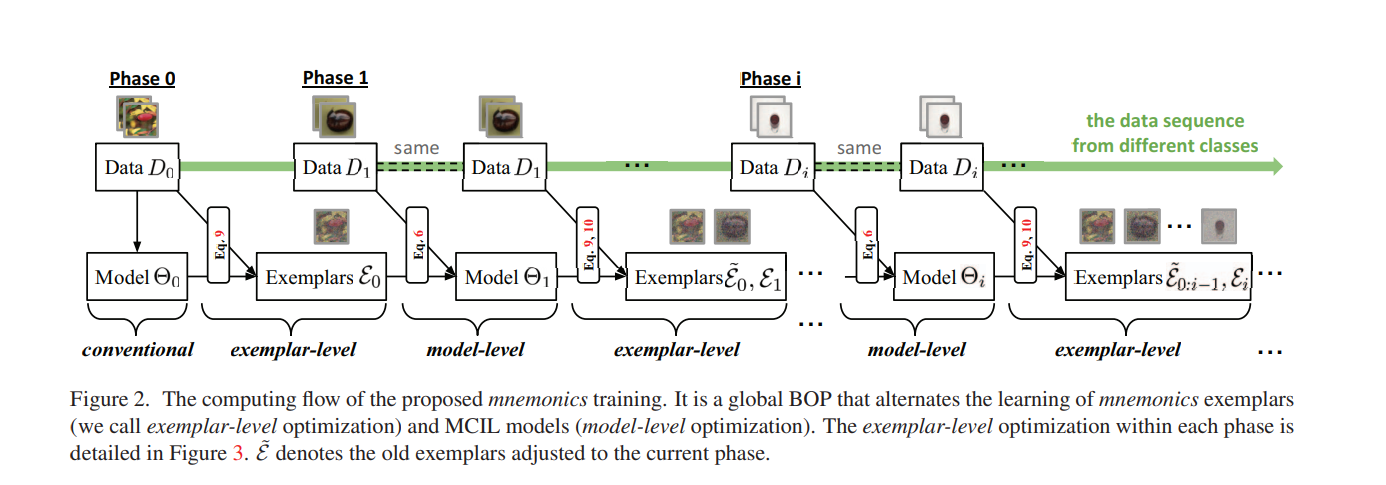
训练过程
$$L_{all} = \lambda L_c(\Theta_i;\varepsilon_{0:i-1}\bigcup D_i)+(1-\lambda)L_d(\Theta_i;\Theta_{i-1};\varepsilon_{0:i-1}\bigcup D_i) \tag{5}$$
$$\Theta_{i}\leftarrow\Theta_i-\alpha_1\nabla L_{all} \tag{6}$$
$$\varepsilon_i\leftarrow\varepsilon_i-\beta_i\nabla_{\varepsilon}L_c(\Theta_i^{'};D_i) \tag{9}$$
$$\varepsilon_{0:i-1}^{A}\leftarrow\varepsilon^A_{0:i-1}-\beta_2\nabla_{\varepsilon^A}L_c(\Theta^{'}_i(\varepsilon^A_{0:i-1});\varepsilon^B_{0:i-1}) \tag{10a}$$
$$\varepsilon_{0:i-1}^{B}\leftarrow\varepsilon^B_{0:i-1}-\beta_2\nabla_{\varepsilon^B}L_c(\Theta^{'}_i(\varepsilon^B_{0:i-1});\varepsilon^A_{0:i-1}) \tag{10b}$$
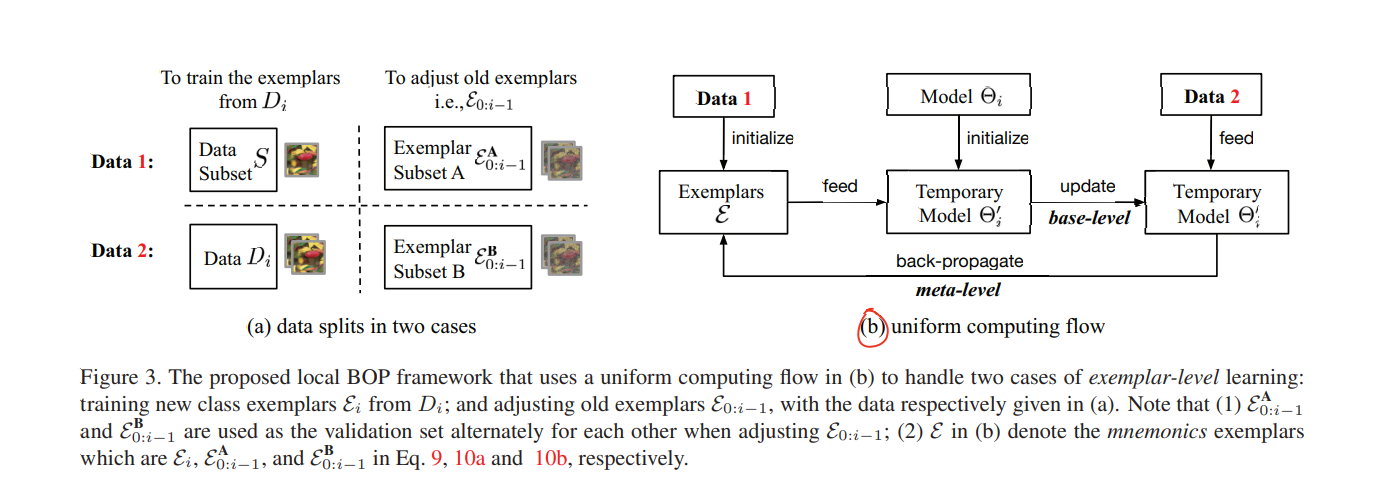
其中,$L_c$是 softmax交叉熵损失,$L_d$是蒸馏损失。这里的$\Theta_i^{'}$是用$\varepsilon$训练一个临时模型以最大化对$D_i$的预测。之后固定$\Theta_i^{'}$即可实现对数据集的优化。公式10把留存的样例集分为两个子集,分别作为对方的验证集。
训练流程很清晰:在优化模型参数$\Theta$时,同时计算了交叉熵损失和蒸馏损失;而优化样例集$\varepsilon$时,只计算了交叉熵损失。利用一个临时模型$\Theta_i^{'}$来优化样例集的优势在于,这能使得保留的数据理论上包含更多旧模型知识——**对于$\varepsilon_i$而言,$\Theta_i^{'}$基于$D_i$优化,所以以其为参数优化样例集$\varepsilon_i$可以使$\varepsilon_i$包含更多的$D_i$的特征;对于$\varepsilon_{0:i-1}$而言,基于$\Theta_i^{'}$的优化可以让它们集成$D_i$的特征**。
个人感受:本文有趣的地方就在于利用训练好的模型去优化留存的数据,从而让数据更具代表性。不过使用最新的模型去优化以前留存的数据,这带来的一个直观问题是:旧数据虽然集成了新模型的知识,但理论上却也损失了其对旧数据的代表性。
模型框架
下图直观的展示了本文的核心部分——如何训样例集$\varepsilon$。
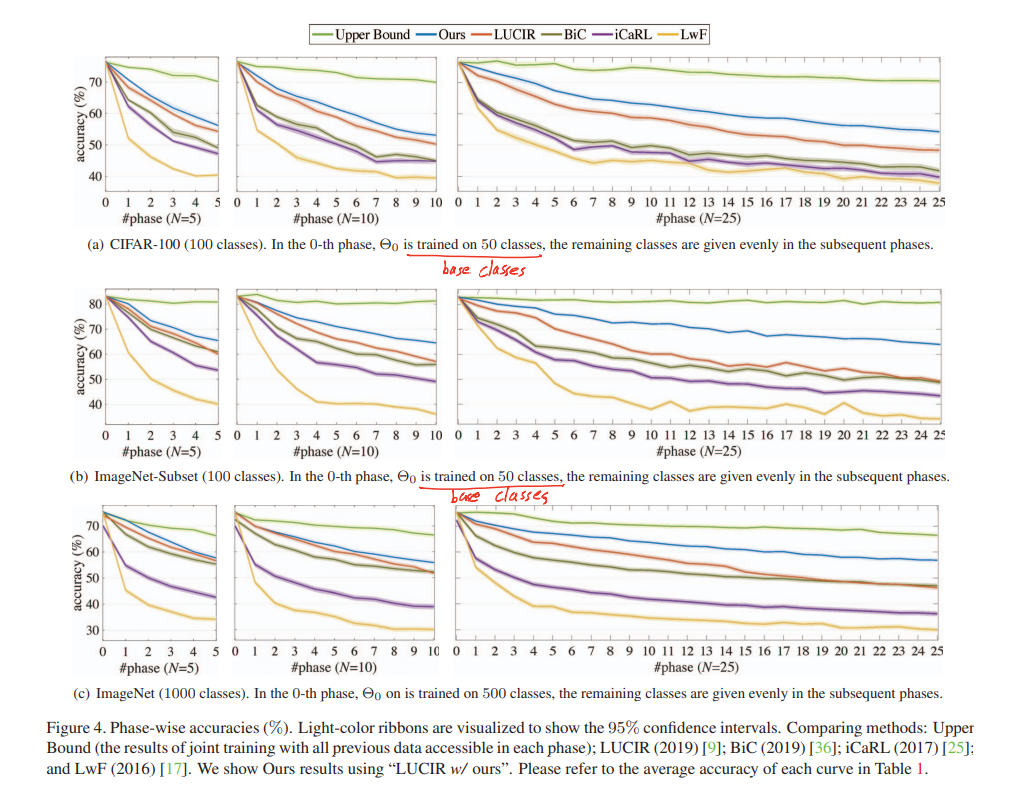
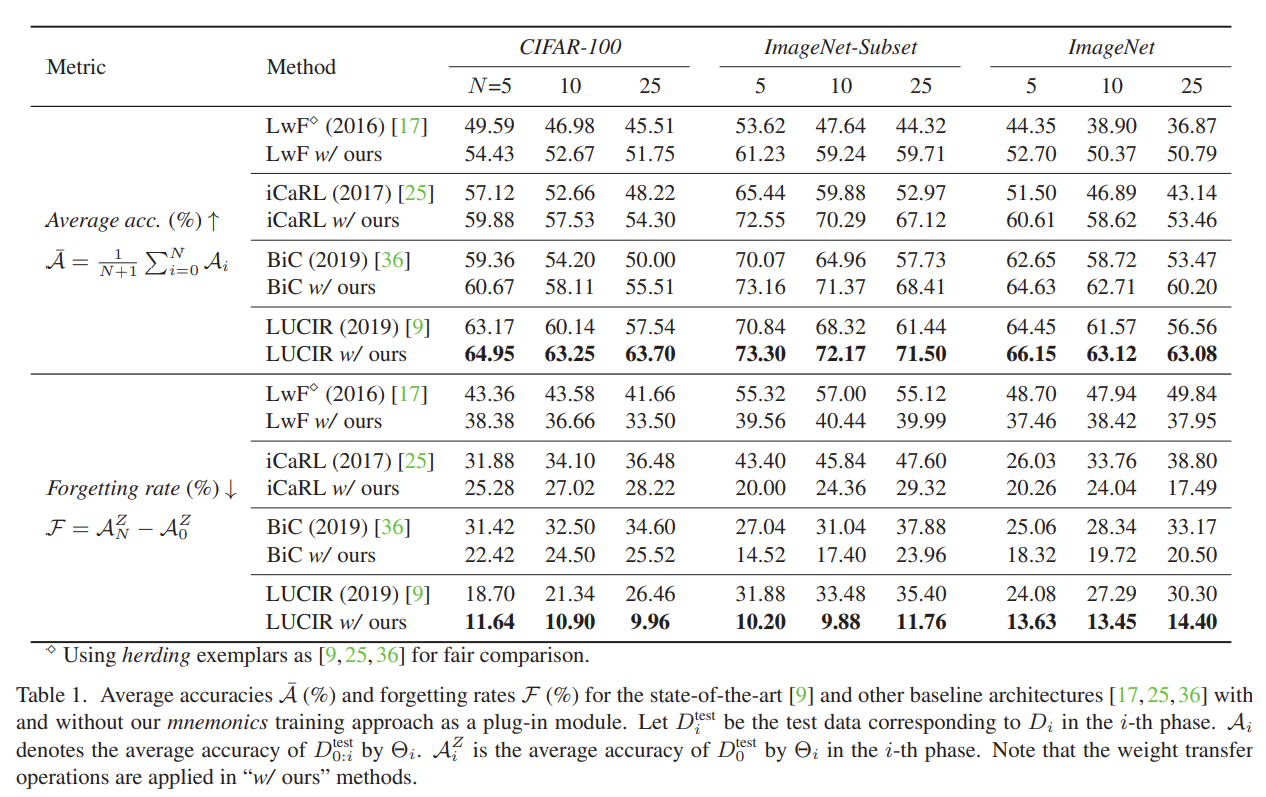
实验结果
以一半的类作为第一次训练的基准,之后按照阶段 N = 5, 10, 25 进行增量训练