一、简介

本文发表于 CVPR 2021，随文代码见此。（本文是西交数学与统计学院发表的文章，数学方面比较硬核）

本文专注于连续训练时不访问之前的数据。本文首先分别针对深度网络在持续学习中的稳定性和可塑性提出了两个理论条件。 基于它们设计了一种新的网络训练算法，称为 Adam-NSCL 用于持续学习，它迫使网络参数更新位于每个网络层的先前任务输入特征的零空间中，如 Fig1 所示。

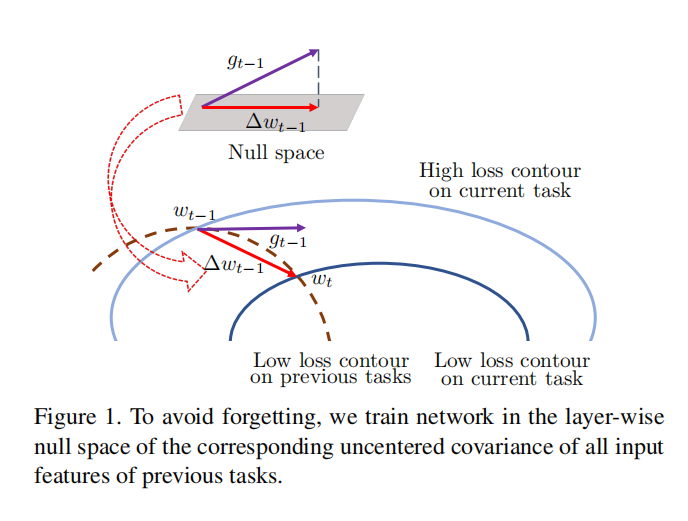
输入特征的分层零空间可以建模为特征的非中心协方差的零空间，该协方差可以在学习每个任务后递增计算。由于保证零空间的存在过于严格，故本文用输入特征非中心协方差的最小奇异值对应的奇异向量跨越的子空间来近似每一层的零空间。本文将该策略嵌入到 Adam 优化算法中，将Adam生成的候选参数更新逐层投影到近似的零空间中。

输入特征分层零空间 （The layer-wise null space of input feature) 指的应该是特征图为零的位置

特征的非中心协方差 我们可以正常计算得到特征的协方差，并对其进行去中心化。本文用最小奇异值对应的奇异向量来近似

总结而言，本文基于正则化思想，采取约束模型的参数更新的方式来保证模型的特征学习。结构上，所有任务共享同一个主干网络，但每个任务都有自己的分类器。 模型在相应的任务上训练后，分类器将被固定。（multi-head classifier）

基于这种设计的增量学习算法显示的分割了不同任务的分类空间，从而避免特征空间的模糊所带来的麻烦。但这类设计的缺点也很明显——需要在推断时被告知 task-id，否则就需要额外设计判别器区分 task-id。前者很难在实际中生效（如果需要提供task-id来分割任务，为何不干脆训练一个针对新任务的模型呢？）；后者则再次面临特征模糊的问题，解决难度不亚于 single-head classifier

二、 分析稳定性和可塑性

1. conditions for continual learning

Condition 1 (stability). 对于 $l = 1, · · · , L,$ 当 $f$ 在任务 $T_t$ 上被训练时，$Δw^l_{t,s}$ 在每个训练步骤 $s$ 应该位于无中心特征协方差矩阵 $\overline{X}^l_{t−1}$ 的零空间中，即，

$$\overline{\chi}^l_{t−1}∆w^l_{t,s} = 0. \quad(3)$$

其中，$∆w^l_{t,s}$​表示 $s$​​ 阶段网络参数的变化量

Condition 2 (scalability). 假设网络 $f$​​​ 正在接受任务 $T_t$​​​ 训练，且 $g_{t,s}=\left{g^1_{t,s},…,g^L_{t,s}\right}$​​​ 表示在 $s$​​​ 阶段训练 $f$​​​ 经梯度下降算法生成的参数更新。$<∆w_{t,s}, g_{t,s} > > 0$​​​​ 应该成立，其中 $<·， ·> $​​​​代表内积

详细的数学推导这里就略过了，简单概括一下：condition 1 的内在逻辑是让参数的更新在特征的非中心协方差的零空间中，这样的好处是降低参数更新对于原特征的影响，从而保护稳定性（奇异值小的空间对原矩阵的影响较小）；condition 2 的 $<.,.>$​ 表明梯度更新方向与参数变化量相似，即梯度是朝着最小化损失的方向前进的，从而保护了伸缩性。

又因为实际上并不能去衡量零空间，所以本文采取了 Algorithm 2 的近似方法。

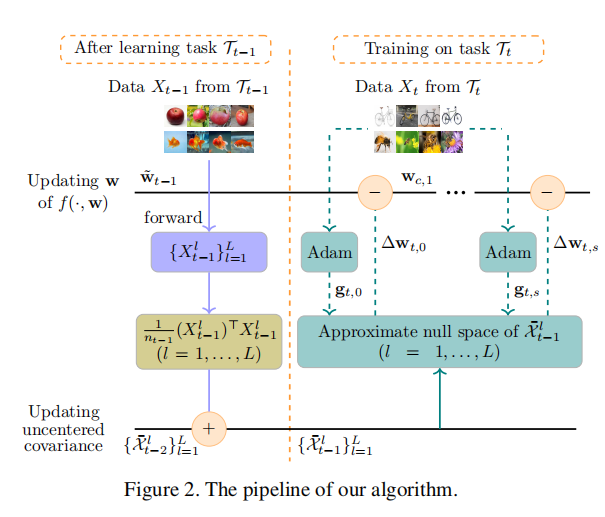
实验

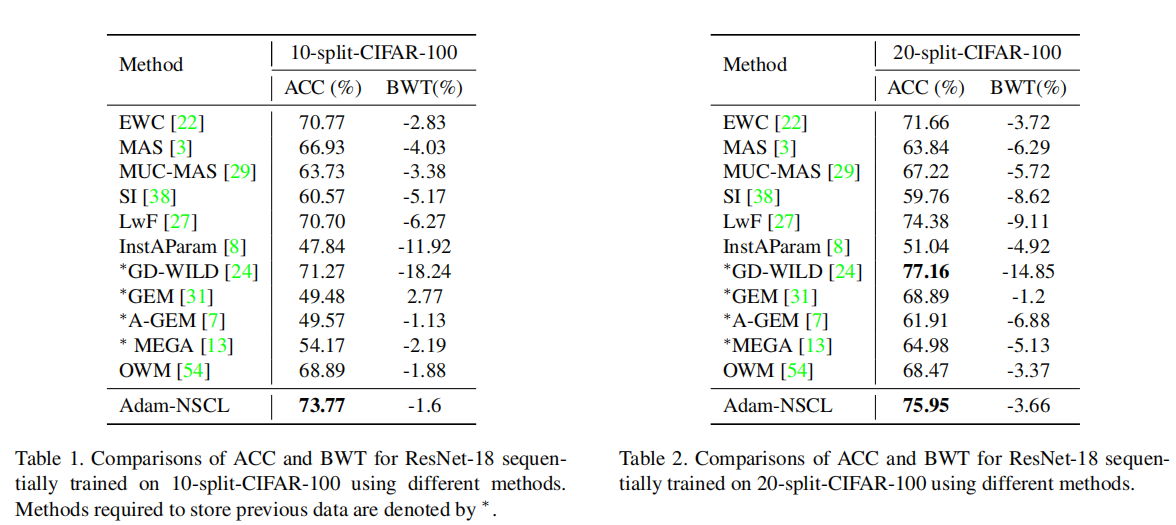
相当硬核的一篇数学想机器学习论文，文章最大的特点就是数学层面的“假设、近似、推导”。核心还是正则化的思想，旨在约束模型参数。

在我的理解里，文中提到的“特征的去中心协方差矩阵的零空间”中的“去中心”应该是修饰词，意为寻找最影响力最小的特征，所以就有了“零空间”的说法。因此也就有了本文提到的利用最小奇异值对应的向量来近似这个零空间。抓住“零空间影响力小”这一内核，那么本文的 insight 还是从参数约束的角度考虑。

附录

奇异值 矩阵的一种概念，一般通过奇异值分解定理求得。奇异值往往对应着矩阵中隐含的重要信息，且重要性和奇异值大小正相关。每个矩阵 $A$​ 都可以表示为一系列秩为1的“小矩阵”之和，而奇异值则衡量了这些“小矩阵”对于 $A$ 的权重。